买房子
题目描述
有天小C突发奇想,自己是不是也该考虑一下买房子的问题了。小C所在的城市被划分成n个区域,这n个区域是连通的,并且从任意一个区域到达另外区域的方案数只有一种。现在这n个区域都有房卖,小C想,如果他要选择买房区域的话,他所在的区域到其他的区域的距离总和应该最小。现在告诉你n个区域的连接情况,请你帮他算算,有多少个区域满足要求?
输入格式
输入第一行,一个整数n;
接下来n-1行,每行三个整数a,b,c,表示连接区域a和b的路长为c,其中0<=a,b< n,0< c<=10000。
输出格式
输出满足条件的区域数和最小的距离总和。
样例
输入
6
0 1 1
1 5 1
1 2 2
2 3 1
2 4 1
输出
2 10
数据范围与提示
对于40%的数据,1< n<=200;
对于60%的数据,1< n<=2000;
对于100%的数据,1< n<=20000。
解析
树的遍历顶级题。样例图如下所示。
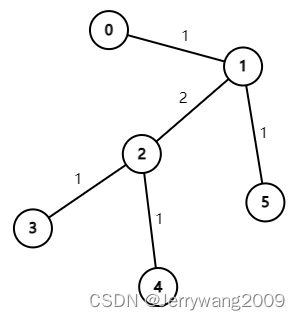
可以分开为一个个子树进行考虑。我们假设小 C 房子买在 $0$ 位,这样树的根节点就是 $0$。先跑一遍 $dfs$,记录每个子树的深度和权值 $pre$ 数组。搜索结束后,房子买在 $0$ 位的距离总和 就是 $pre_0$。
重点在于下面的换根操作。再次 $dfs$ 枚举换过之后的根。以下公式很容易看出。$w$ 是连接这两个子树的边权。 $$ sum_v=sum_u-siz_v\times w+(n-siz_v)\times w $$ 就像这样。以下是一个从根 $1$ 换到根 $2$ 的例子。
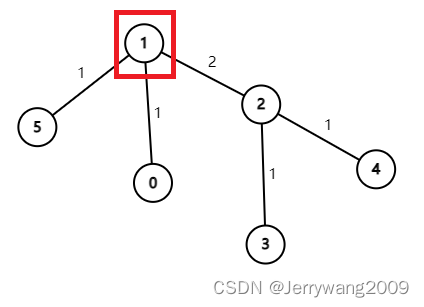
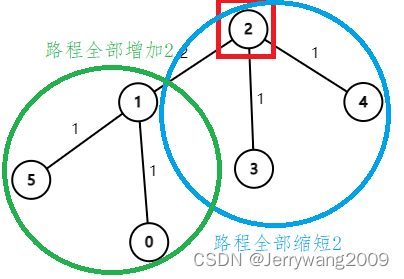
最后打擂台求 $sum$ 的最小值即可。
代码
// C
#include <bits/stdc++.h>
#define int long long
#define SIZE 20010
#define all(x) x.begin(), x.end()
#define debug(x) cout<<#x<<":"<<x<<endl;
using namespace std;
struct node
{
int u, w;
};
vector<node> a[SIZE];
int siz[SIZE]={0}, sum[SIZE]={0}, pre[SIZE]={0};
int n;
void calc(int u, int f)
{
siz[u]=1;
for(auto t:a[u])
{
int v=t.u;
int w=t.w;
if(v==f) continue;
calc(v, u);
siz[u]+=siz[v];
pre[u]+=pre[v]+w*siz[v];
}
}
void dfs(int u, int f)
{
for(auto t:a[u])
{
int v=t.u;
int w=t.w;
if(v==f) continue;
sum[v]=sum[u]-siz[v]*w+(n-siz[v])*w;
dfs(v, u);
}
}
signed main()
{
cin>>n;
for(int i=0; i<n-1; i++)
{
int u, v; cin>>u>>v;
int w; cin>>w;
a[u].push_back({v, w});
a[v].push_back({u, w});
}
calc(0, -1);
sum[0]=pre[0];
dfs(0, -1);
int Min=LLONG_MAX;
for(int i=0; i<n; i++)
Min=min(Min, sum[i]);
int cnt=0;
for(int i=0; i<n; i++)
cnt+=sum[i]==Min;
cout<<cnt<<" "<<Min;
return 0;
}